728x90
반응형
목적에 따른 손실 함수(Loss Function)
평균제곱오차 (MSE: Mean Square Error,)
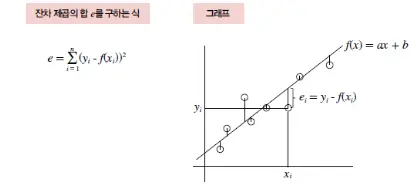
예측을 위한 손실 함수
$$E = \dfrac{1}{n}\sum^{n}_{i=1}(y-\widehat{y})^2$$
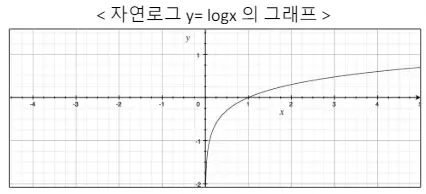
Cross-Entropy Error
분류를 위한 손실함수
$$E = \sum^i_{k=1}t_{k}log_{e}y_{k}$$
$y$는 신경망의 출력, $t$는 정답 레이블
다중분류에서 적용되는 방법
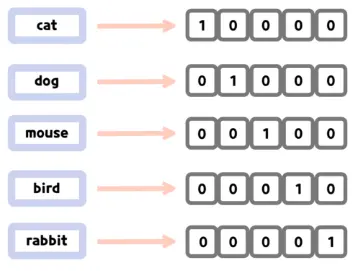
One-Hot Encoding
분류를 위한 손실함수를 사용하기 위한 준비
Example
경사하강법 (GD: Gradient Descent OPtimization)
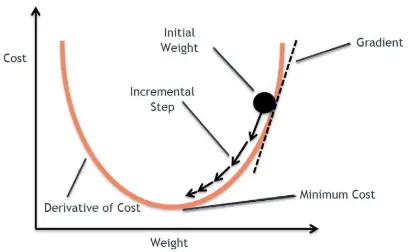
- 딥러닝에선 네트워크 파라미터에 대해 실제값($y$)과 예측값($\widehat{y}$)의 차이를 정의하는 Loss Function을 최소화하기 위해 기울기를 이용하여 Loss Function을 최소화하도록 네트워크가 학습 됨
- 네트워크의 학습에선 $\theta$에 대해 gradient 반대 방향으로 일정 크기만큼 이동하는 것을 반복(Epoch) 하며 Loss Function의 값을 최소화할 수 있게 하는 파라미터 $\theta$를 찾게 됨
- 지금 기울기 = 이전 기울기가될 때까지 반복(최소화 완료)
- $\theta$에 대한 식을 일반화하면 아래와 같음
$\theta = \theta - lr * Gradient$ $= \theta - lr * \partial(\theta)$
핵심은 $\partial(\theta)$을 0으로 만드는 것

'얼마나 업데이트 할 것인가'를 결정하는 leanrin_rate(학습률)
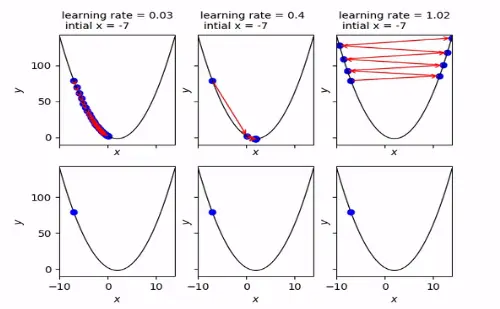
- learning_rate가 너무 크면 발산하게 됨 (최적화 불가)
- leanring_rate가 작을수록 최적화에 유리함
- 다만, 너무 작게되면 학습이 오래걸리게 됨
활성화함수(Activation Function)
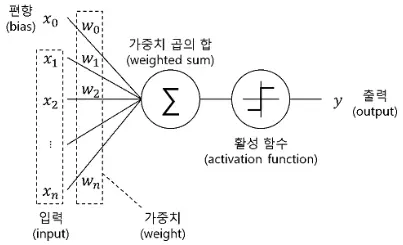
활성화함수란?
인공 신경망의 입력 값을 변환하는 함수
$$Activation(w_{n}x_{n}) = \widehat{y}$$
활성화 함수는 비선형
다층 신경망 구조에서 층별 연산 특징을 유지하기 위함
- 최적의 경계선(Gradient, $\partial(\theta)$)을 찾기 위한 미분이 필요하기 때문
- 따라서 미분이 가능한 활성화 함수를 만들어야 함
다양한 활성화 함수

- 최근에는 layer를 많이 쌓기 때문에 $w_{n}x_{n}$값이 0보다 작은 노드는 아예 비활성화 시키는 ReLU가 각광받는 추세
- Sigmoid는 layer가 많으면 특징이 편향되는 경향이 있음. 주로 마지막 layer에서 사용
출처: [성균관대 컨소시엄] 건양대 DNA School 기초과정 - 병원 임상데이터를 활용한 AI기초 강의자료
728x90
반응형
'Data Science > ML & DL' 카테고리의 다른 글
| 이미지를 위한 인공지능, CNN (0) | 2024.07.10 |
|---|---|
| 인공지능을 위한 평가방법 Mextics(Accuracy, Confusion Matrix, ROC, AUC (0) | 2024.07.09 |
| 선형(Linear) 문제 (0) | 2024.07.07 |
| 기계학습의 종류 (1) | 2024.07.05 |
| 인공지능의 역사 (0) | 2024.07.04 |
