728x90
반응형
두 변수의 상관관계

- 데이터를 다룰 때 데이터를 구성하는 항목을 변수라고 함
- 데이터에서 변화를 나타내는 한 가지 이상의 변수 쌍 또는 변수 쌍을 사용한 계산 식을 feature(특징량)라고 함
- 통계표에서 변수 2개(feature)를 선택해 산포도를 그리고 모델을 도출
선형 문제로 무엇을 할 수 있고, 어떻게 표현되는가?

- 변수 값 쌍이 있을 때 변수 값 각각을 그래프의 X축과 Y축 값으로 정한 후 각 값이 만나는 곳에 점을 찍으면 변수 값 쌍들의 분포를 파악해볼 수 있음(산포도)
- 점의 분포를 선형 함수의 제약과 조건을 이용해 구할 수 있는 문제를 선형 계획 문제라고 함
- 선형 함수를 이용해 점의 분포를 여러 개 그룹으로 나눌 수 있을 때를 "선형 분리할 수 있다"라고 함
선형 문제란
데이터에서 선형으로 된 규칙을 찾는 방법
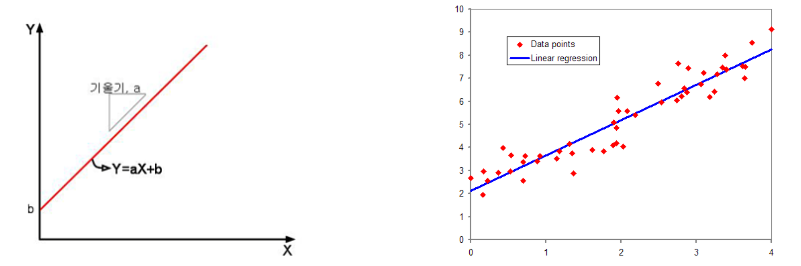
- 선형은 수학에서 나타내는 1차식 or 1차 함수 ($y=ax+b$)
- 즉, 선형이란 그래프의 형태가 1개의 직선으로 표현된다는 뜻
- 1개의 일정한 기울기를 가지고 기울기의 변화가 없는 것은 선형
비선형 문제
현실 세계에 데이터에서 규칙을 찾는 방법
선형이 아닌 문제
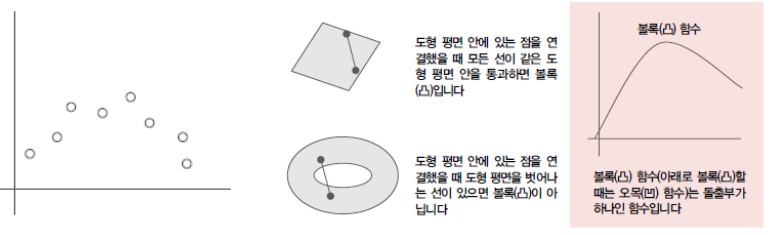
- 변수 값 쌍을 점 형태로 나타낼 수 있다면, 함수 형태로 변환된 것을 '사상'이라고 함
- 사상 개념(산포도)으로 대응할 수 없을 때는 비선형분포로 취급함
- 비선형분포를 다룰는 문제를 비선형 문제라고 함. 비선형 계획법을 이용해 해결할 수 있음 (ex, 정규분포)
비선형 문제란
비선형은(Nonlinear)은 1개의 직선으로 표현되지 않는 모든형태. 즉, 1차 방정식으로 표현되지 않는 모든 형태를 비선형이라고 함


- 비선형은 2개 이상의 기울기를 가짐
- 기울기가 임의의 조건에 의해 변한다면 비선형
회귀 분석
한 바퀴 돌아서 본디의 자리나 상태로 돌아오는 분석방법
- 회귀분석은 주어진 데이터로 어떤 함수를 만들어 낸 후, 이 함수를 피팅하는 작업(회귀)임
- 가장 기본적인 회귀분석은 요소들 사이의 비례 관계를 활용하는 단순 회귀 분석임
- ex) 신장과 체중 사이 관계, 임대주택 방 크기와 임대료 사이의 관계
- 회귀직선의 기울기와 절편 구하기
다중 회귀
독립 변수가 1개일 때의 회귀 분석을 단순 회귀 분석이라고 하며, 독립 변수가 여러 개인 경우의 회귀분석은 다중 회귀 분석
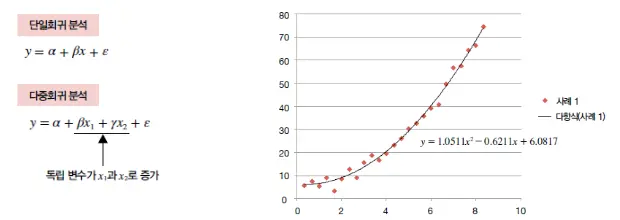
- 다중 회귀 분석은 독립 변수가 여러 개이므로 단순 회귀 분석처럼 2차원 그래프로 시각화하기는 어려움
- 이런 경우 2차원 평면상에 점을 찍을 수 있도록 주성분 분석을 이용함
단순선형회귀 vs 다중선형회귀
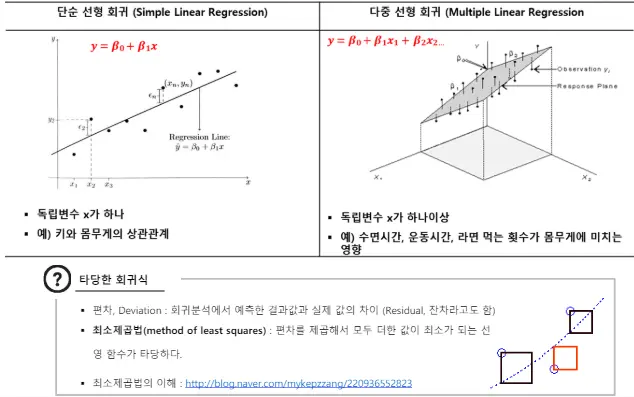
최소 제곱법 (Least Square Method)
회귀분석에서 함수에 피팅할 때는 편차가 최소화되도록 함수를 조정
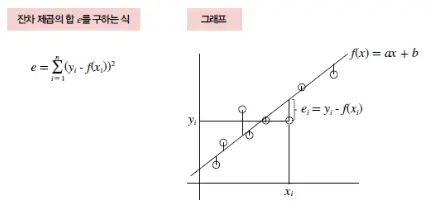

- 이때 가장 일반적으로 사용하는 방법은 최소제곱법
- 최소제곱법 식과 그래프
최소제곱법의 한계
- 특이점에 취약함
가중 회귀분석
- 최소제곱법은 특이값에 취약하다는 약점이 있음
- 특이값에 패널티를 부여하거나 아예 제외하는 방법 등으로 수정해야 함
- LOWESS(Robust) 회귀
- 어떤 한 지점에 가중회귀 함수를 사용해 평활화를 실행한 회귀 식 도출 방법

로지스틱 회귀 (Logistic Regression)

- 영국의 통계학자인 D. R. Cox가 1958년에 제안한 확률 모델로서 독립 변수의 선형 결합을 이용하여 사건의 발생 가능성(확률, probability)을 예측하는데 사용되는 통계 기법
- 로지스틱 회귀의 목적은 일반적인 회귀 분석의 목표와 동일하게 종속 변수와 독립 변수 간의 관계를 구체적인 함수로 나타내어 향후 예측 모델에 사용하는 것
- 하지만 로지스틱 회귀는 선형 회귀 분석과는 다르게 종속 변수가 범주형 데이터(O/X) 를 대상으로 하며 입력 데이터가 주어졌을 때 해당 데이터의 결과가 특정 분류로 나뉘기 때문에 일종의 분류 기법으로도 볼 수 있음
- 종속 변수에 약간의 수정을 가한 선형회귀로 다항식 회귀처럼 일반화 선형 모델의 하나로 분류
로지스틱 회귀 분석 활용 예

- 연속형 자료에 따른 범주형 자료의 영향력을 파악하기 위함
- Ex) 독립변수: [정치참여도, 여당선호도, 야당선호도 (모두 5점 척도)] 종속변수: 선거참여여부(참여/비참여)
- 선형회귀의 종속변수는 일반적으로 연속적이지만, 만약 종속변수가 범주형이라면 로지스틱 회귀를 사용한다.
출처: [성균관대 컨소시엄] 건양대 DNA School 기초과정 - 병원 임상데이터를 활용한 AI기초 강의자료
728x90
반응형
'Data Science > ML & DL' 카테고리의 다른 글
| 인공지능을 위한 평가방법 Mextics(Accuracy, Confusion Matrix, ROC, AUC (0) | 2024.07.09 |
|---|---|
| 딥러닝의 원리와 확장성 (0) | 2024.07.08 |
| 기계학습의 종류 (1) | 2024.07.05 |
| 인공지능의 역사 (0) | 2024.07.04 |
| 인공지능이란? (0) | 2024.07.04 |
