[혼공머] Chapter 03-2. 선형 회귀

K-Neighbors Regressor을 이용해 학습시킨 모델에 문제가 발생했다!

---

데이터셋

 

perch_length = np.array([8.4, 13.7, 15.0, 16.2, 17.4, 18.0, 18.7, 19.0, 19.6, 20.0, 21.0,
       21.0, 21.0, 21.3, 22.0, 22.0, 22.0, 22.0, 22.0, 22.5, 22.5, 22.7,
       23.0, 23.5, 24.0, 24.0, 24.6, 25.0, 25.6, 26.5, 27.3, 27.5, 27.5,
       27.5, 28.0, 28.7, 30.0, 32.8, 34.5, 35.0, 36.5, 36.0, 37.0, 37.0,
       39.0, 39.0, 39.0, 40.0, 40.0, 40.0, 40.0, 42.0, 43.0, 43.0, 43.5,
       44.0])

perch_weight = np.array([5.9, 32.0, 40.0, 51.5, 70.0, 100.0, 78.0, 80.0, 85.0, 85.0, 110.0,
       115.0, 125.0, 130.0, 120.0, 120.0, 130.0, 135.0, 110.0, 130.0,
       150.0, 145.0, 150.0, 170.0, 225.0, 145.0, 188.0, 180.0, 197.0,
       218.0, 300.0, 260.0, 265.0, 250.0, 250.0, 300.0, 320.0, 514.0,
       556.0, 840.0, 685.0, 700.0, 700.0, 690.0, 900.0, 650.0, 820.0,
       850.0, 900.0, 1015.0, 820.0, 1100.0, 1000.0, 1100.0, 1000.0,
       1000.0])

from sklearn.model_selection import train_test_split

# 훈련 세트와 테스트 세트로 나눕니다
train_feature, test_feature, train_target, test_target = train_test_split(perch_length, perch_weight, random_state=42)

# 훈련 세트와 테스트 세트를 2차원 배열로 바꿉니다
train_feature = train_feature.reshape(-1, 1)
test_feature = test_feature.reshape(-1, 1)

 

---

K-Neighbor Regressor 모델 훈련 (n_neighbors=3)

 

from sklearn.neighbors import KNeighborsRegressor

knr = KNeighborsRegressor(n_neighbors=3)    # k-최근접 이웃 회귀 모델을 만듭니다
knr.fit(train_feature, train_target)    # k-최근접 이웃 회귀 모델 훈련

 

 

---

길이가 50cm인 농어 무게 예측

 

# 길이가 50cm인 농어의 무게를 예측
print(f'길이 50cm인 농어 무게 Predict: {knr.predict([[50]])}')

길이 50cm인 농어 무게 Predict: [1033.33333333]

• 예측 결과: 1,033g
• 하지만 길이가 50cm인 농어의 실제 무게는 훨씬 더 많이 나간다! -> 모델이 틀림

---

Train 데이터셋에 있는 농어, 50cm 농어와 이웃을 Scatter Plot 표현

 

distance, indexes = knr.kneighbors([[50]])    # 50cm 농어의 이웃을 구합니다
plt.scatter(train_feature, train_target)    # 훈련 세트의 산점도를 그립니다
plt.scatter(train_feature[indexes], train_target[indexes], marker='D')    
# 이웃 샘플을 다시 그립니다

plt.scatter(50, 1033, marker='^')    # 50cm 농어 데이터
plt.xlabel('length')
plt.ylabel('weight')
plt.legend(['Train data', 'Neighbor data', '50cm data'])
plt.show()

 

output

 

---

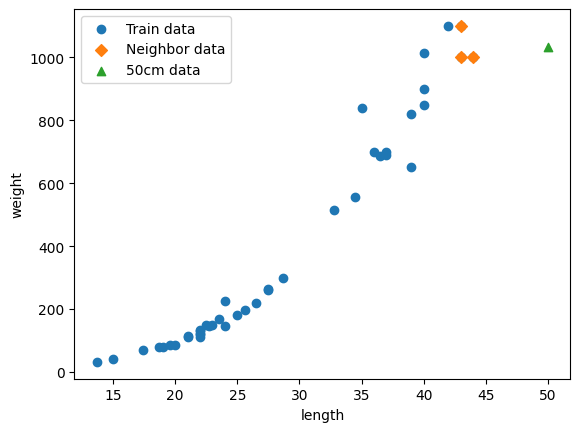
50cm 농어 이웃들의 평균

 

# 이웃 샘플의 타깃의 평균을 구합니다
print(f"50cm농어 이웃들의 평균: {np.mean(train_target[indexes])}")   

50cm농어 이웃들의 평균: 1033.3333333333333

 

-> 예측 데이터가 Train_data의 범위를 벗어나면 엉뚱한 값을 예측하네?

 

---

100cm 농어에 대한 예측도 똑같을까?

 

 # 길이가 100cm인 농어의 무게를 예측
print(f'길이 100cm인 농어 무게 predict: {knr.predict([[100]])}')   

길이 100cm인 농어 무게 predict: [1033.33333333]

distance, indexes = knr.kneighbors([[100]])    # 100cm 농어의 이웃을 구합니다
plt.scatter(train_feature, train_target)    # 훈련 세트의 산점도를 그립니다
plt.scatter(train_feature[indexes], train_target[indexes], marker='D')    # 이웃 샘플을 다시 그립니다

plt.scatter(100, 1033, marker='^')    # 100cm 농어 데이터
plt.xlabel('length')
plt.ylabel('weight')
plt.legend(['Train data', 'Neighbor data', '100cm data'])
plt.show()

 

output

 

결론: K-Neighbors Regressor(K-최근접 회귀) 모델을 사용해 예측했을 때, 예측값이 훈련 데이터셋의 범위를 넘어가면 예측을 못한다!!

 

-> 선형 회귀(Linear Regression) 모델을 사용해보자

 

---

 

선형 회귀 (Linear Regression)

 

• 대표적인 회귀 알고리즘
• 비교적 간단하고 성능이 뛰어남
• 선형이란 말에서 짐작할 수 있듯이 특성이 하나인 경우, 어떤 직선을 학습하는 알고리즘
• 학습 데이터의 특성에서 규칙을 발견해, 가장 잘 나타낼 수 있는 직선을 찾음

 

단순 선형 회귀 분석 (Simple Linear Regression)

 

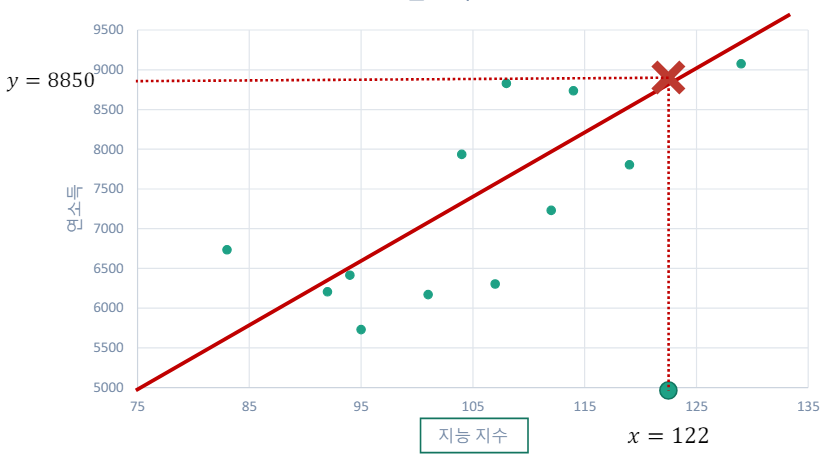
• 지능지수($X$)와 연소득($Y$)에 선형관계가 있다고 가정
  • $y\approx \theta +\theta X$
• $F\left( x\right) =\theta +\theta _{i}X$ 에서
  • 적절한 $\theta _{0}$(절편), $\theta _{1}$(기울기)를 찾은 후,
• 지능지수가 122일 때 예상되는 연소득 값?
  • $\widehat{Y}=\theta +\theta _{1}X=8850$ 으로 예측

• 선형 회귀 분석에서는 적절한 $\theta _{0}, \theta _{1}$을 찾는 것이 중요!
• 적절함의 기준이 필요하다.
  • 빨강 -> 경향과 맞지 않는다, 주황 or 갈색 중에서는 누가 더 좋을까?

 

---

 

Simple Linear Regression 모델 훈련

 

from sklearn.linear_model import LinearRegression

lr = LinearRegression()    # 선형 회귀 모델을 만듭니다
lr.fit(train_feature, train_target)    # 선형 회귀 모델을 훈련합니다
print(f'길이 50cm인 농어 무게 Predict: {lr.predict([[50]])}')    # 길이가 50cm인 농어의 무게를 예측

길이 50cm인 농어 무게 Predict: [1241.83860323]

 

-> K-최근접 이웃 회귀와 달리, 선형 회귀 모델을 더 무겁게 예측한 것을 볼 수 있다.

---

 

Simple Linear Regression 모델 원리

 

 

• 직선의 방정식: $y = ax + b$
  • $x$: 농어의 길이
  • $y$: 농어의 무게
  • 머신러닝에서는 여기서의 $a$(기울기), $b$(절편)을 파라미터(parameter)라고 부른다.
  • 머신러닝에서는 기울기 $a$를 계수(coefficient) 또는 가중치(weight)라고 부른다.

# 모델 파라미터들의 값 확인
print(f'coef: {lr.coef_}, intercept: {lr.intercept_}')

coef: [39.01714496], intercept: -709.0186449535474

---

 

위에서 구한 기울기와 절편으로 15~50까지의 직선, Train 데이터셋 산점도 그리기

 

# 훈련 세트의 산점도를 그립니다
plt.scatter(train_feature, train_target)   
# 15cm에서 50cm까지 직선을 그립니다
plt.plot([15, 50], [15*lr.coef_+lr.intercept_, 50*lr.coef_+lr.intercept_])    

plt.scatter(50, 1241.8, marker='^')    # 50cm 농어 데이터
plt.xlabel('length')
plt.ylabel('weight')
plt.legend(['Train data', '50cm data'])
plt.show()

 

output

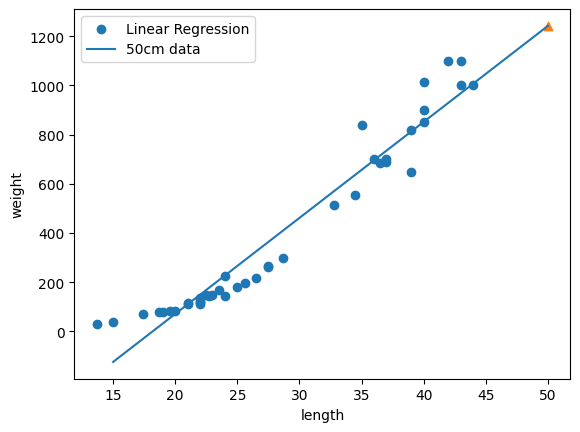
• 선형 회귀 모델이 Train 데이터셋에서 찾은 최적의 직선을 확인할 수 있음
• 길이가 50cm인 농어에 대한 예측은 찾은 직선의 연장선에 위치함
• K-최근점 알고리즘과 다르게, Train 데이터셋의 범위에서 벗어난 데이터도 예측 가능!

 

---

 

R^2 Score 확인

 

# 훈련 세트의 R^2 점수를 확인
print(f'R^2 by Train data: {lr.score(train_feature, train_target)}')    

# 테스트 세트의 R^2 점수를 확인
print(f'R^2 by Test data: {lr.score(test_feature, test_target)}')    

R^2 by Train data: 0.9398463339976041
R^2 by Test data: 0.824750312331356

• Train 데이터셋에 대한 R^2 Score가 높지 않은 것으로 보아, 과소적합되었다고 볼 수 있음
• 또한 그래프의 좌측 하단을보면 무게를 0이하로 예측하는 것을 보아, 조금 잘못된 것을 알 수 있음.

---

 

다중 회귀 (Mutiple Linear Regression)

 

 

• 단순 선형 회귀 분석
  • 하나의 독립변수 $X$로 종속 변수 $Y$를 예측한다
    • F: IQ -> 연봉
    • F: 나이 -> 연봉
• 다중 선형 회귀 분석
  • 동시에 여러 개의 독립변수 $X_{1}, X_{2}, ... X_{d}$를 활용하여 $Y$를 예측
    • F: (IQ, 나이, 성별) -> 연봉
• 일반적으로 다중 선형 회귀 분석이 더 정확!
  • 더 많은 종류의 정보를 활용해서 예측하기 때문

 

• 전반적으로 단순 선형 회귀와 매우 유사
• $연봉 = \theta + \theta _{1} * IQ + \theta _{2} * 나이 + \theta _{3} * 성별$
• $\widehat{y}=\theta {0}+\theta _{1}x{1}+\theta {2}x{2}+\theta {3}x{3}$
• 적절한 매개변수 $W^{T}=\left[ \theta _{0},\theta _{1},...,\theta _{3}\right]$를 찾는 것이 목표

---

 

Multiple Linear Regression 원리

 

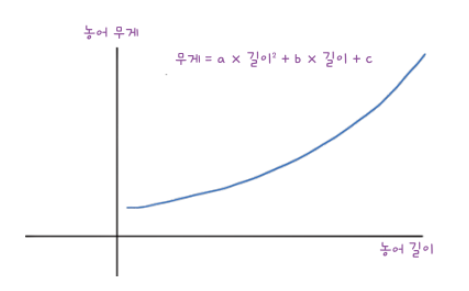
• 2차함수 방정식: $y = ax^{2} + bx + c$
  • $x$: 농어의 길이
  • $y$: 농어의 무게

---

 

데이터를 2차원 배열로 변환

 

# 2차원 배열로 만들기
train_poly = np.column_stack((train_feature**2, train_feature)) 
test_poly = np.column_stack((test_feature**2, test_feature))    

print(f'train_poly.shape: {train_poly.shape}, test_poly.shape: {test_poly.shape}')

train_poly.shape: (42, 2), test_poly.shape: (14, 2)

---

 

다중 회귀 모델 학습

 

lr = LinearRegression()    # 선형 회귀 모델을 다시 만듭니다
lr.fit(train_poly, train_target)    # 2차원 배열로 다시 훈련

# 길이가 50cm인 농어의 무게를 예측
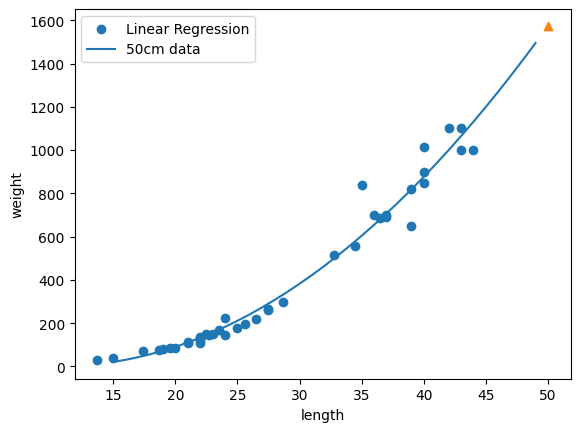
print(f'길이 50cm인 농어 무게 Predict: {lr.predict([[50**2, 50]])}')    

길이 50cm인 농어 무게 Predict: [1573.98423528]

---

 

모델 파라미터 확인

 

print(f'coef: {lr.coef_}, intercept: {lr.intercept_}')

coef: [  1.01433211 -21.55792498], intercept: 116.0502107827827

---

 

위에서 구한 파라미터로 모델의 곡선, Train 데이터의 산점도 그리기

 

point = np.arange(15, 50)    # 15에서 49까지 1차원 배열을 만듭니다
plt.scatter(train_feature, train_target)    # 훈련 세트의 산점도를 그립니다
# 15에서 49까지 예측합니다
plt.plot(point, lr.coef_[0]*point**2 + lr.coef_[1]*point + lr.intercept_)    



plt.scatter(50, 1573.98423528, marker='^')    # 50cm 농어 데이터
plt.xlabel('length')
plt.ylabel('weight')
plt.legend(['Linear Regression', '50cm data'])
plt.show()

 

output

---

 

Train 데이터셋, Test 데이터셋에 대한 R^2 Score 확인

 

# 훈련 세트의 R^2 점수를 확인
print(f'R^2 by Train data: {lr.score(train_poly, train_target)}') 

# 테스트 세트의 R^2 점수를 확인
print(f'R^2 by Test data: {lr.score(test_poly, test_target)}')    

R^2 by Train data: 0.9706807451768623
R^2 by Test data: 0.9775935108325122

• Train 데이터셋과 Test 데이터셋에 대한 R^2 Score가 크게 높아짐
• 하지만 여전히 R^2 score값: Train data < Test data
• 과소적합(Under-fitting)이 남아있음