Chapter 3.3 다차원 배열의 계산

넘파이의 다차원 배열을 사용한 계산법을 숙달하면 신경망을 효율적으로 구현할 수 있다.

그래서 이번엔 넘파이의 다차원 배열 계산에 대해 알아보고 신경망을 구현해보겠다.

3.3.1 다차원 배열

다차원 배열도 기본은 '숫자의 집합'이다. 숫자를 N차원으로 나열하는 것을 다차원 배열이라고 한다.

 

>>> import numpy as np
>>> A = np.array([1, 2, 3, 4])
>>> print(A)
[1 2 3 4]
>>> np.ndim(A)    // np.ndim(): 배열의 차원 수 확인
1
>>> A.shape        // '배열'.shape: 배열의 형상 확인, 무조건 튜플 형태로 반환 
(4,)
>>> A.shape[0]
4

 

2차원 배열은 특히 행렬(matrix)라고 부르고 [그림 3-10]과 같이 배열의 가로 방향을 행(row), 세로 방향을 열(column)이라고 한다.

[그림 3-10] 2차원 배열(행렬)의 행(가로)와 열(세로)

 

---

3.3.2 행렬의 곱

행렬(2차원 배열)의 곱을 구하는 방법을 알아보자. 행렬곱은 [그림 3-11]처럼 계산한다.

 

[그림 3-11] 행렬의 곱 계산 방법

그림처럼 행렬 곱은 왼쪽 행렬의 행과 오른쪽 행렬의 열을 원소별로 곱하고 그 값을 더해서 계산한다. 그리고 그 계산 결과가 새로운 다차원 배열의 원소가 된다.

 

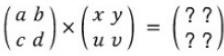
이해가 안간다면 다음 그림을 보면 확실히 이해가 갈 것이다.

 

파이썬으로 행렬곱 구현.

>>> A = np.array([[1,2], [3,4]])
>>> A.shape
(2, 2)
>>> B = np.array([[5, 6], [7,8]])
>>> B.shape
(2, 2)
>>> np.dot(A, B)    
array([[19, 22],
       [43, 50]])

// np.dot(): 행렬 곱 계산(1차원 배열은 벡터, 2차원 배열이면 행렬곱 계산
// !주의!: np.dot(A,B) != np.dot(B,A), 행렬곱은 피연산자 순서가 다르면 결과도 다름!

 

앞에서는 형상이 같은 행렬곱의 예를 보았지만, 형상이 다른 행렬곱도 마찬가지 방법으로 계산 할 수 있다.

 

예를 들어 다음은 \(2\times 3\) 행렬과 \(3\times 2\) 행렬의 곱을 파이썬으로 구현한 것이다.

>>> A = np.array([[1,2,3], [4,5,6]])
>>> A.shape
(2, 3)
>>> B = np.array([[1,2], [3,4], [5,6]])
>>> B.shape
(3, 2)
>>> np.dot(A, B)
array([[22, 28],
       [49, 64]])

\(2\times 3\) 행렬 A와 \(3\times 2\) 행렬 B의 곱은 이와 같이 구현할 수 있다. 이때 '행렬의 형상(shape)'에 주의해야 한다.

 

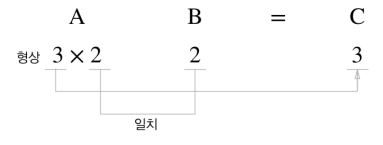
구체적으로 말하면 행렬 A의 '열' 수와 행렬 B의 '행' 수가 같아야 한다. 그렇지 않으면 행렬곱을 계산할 수 없다.

 

[그림 3-12] 행렬의 곱에서는 대응하는 차원의 원소 수를 일치시켜라

[그림 3-12]는 \(3\times 2\) A와 \(2\times 4\) 행렬 B를 곱해 \(3\times 4\) 행렬 C를 만드는 예이다. 계산 결과인 행렬 C의 형상은 행렬 A의 행 수와 행렬 B의 열 수가 된다.

 

A가 2차원 행렬이고 B가 1차원 배열일 때도 [그림 3-13]과 같이 '대응하는 차원의 원소 수를 일치시켜라'는 원칙이 똑같이 적용된다.

[그림 3-13] A가 2차원 행렬, B가 1차원 배열일 때도 대응하는 차원의 원소 수를 일치시켜라.

 

---

3.3.3 신경망에서의 행렬 곱

이제 넘파이 행렬을 써서 신경망을 구현해보자. 이번 예시에서는 [그림 3-14]의 간단한 신경망을 가정해보자.

이 신경망은 편향과 활성화 함수를 생략하고 가중치만 갖는다.

 

 

[그림 3-14] 행렬의 곱으로 신경망의 계산을 수행한다.

이 구현에서도 X, W, Y의 형상을 주의해서 보자. 특히 X와  W에 대응하는 차원의 원소수가 같아야 한다.